physique

cordonnée cylindrique et Coordonnées sphériques

Les coordonnées cylindriques sont notamment utilisées dans de nombreux problèmes de mécanique où l'on considère un objet dans un repère tournant. On peut alors avoir besoin des relations concernant la vitesse et l'accélération.

Pour $\overrightarrow {u_{r}}=\cos \theta \overrightarrow {i}+\sin \theta \overrightarrow {j}$ un vecteur radial et $\overrightarrow {u_{\theta }}=-\sin \theta \overrightarrow {i}+\cos \theta \overrightarrow {j}$ un vecteur orthoradial, les quantités cinématiques, position, vitesse, accélération sont données par :

{\begin{aligned}\overrightarrow {OM}&=r\overrightarrow {u_{r}}+z\overrightarrow {u_{z}}\\{\dot {\overrightarrow {OM}}}&=\overrightarrow {V_{M}}={\dot r}\overrightarrow {u_{r}}+r{\dot \theta }\overrightarrow {u_{\theta }}+{\dot z}\overrightarrow {u_{z}}\\{\ddot {\overrightarrow {OM}}}&=\overrightarrow {\Gamma _{M}}=({\ddot r}-r{\dot \theta }^{2})\overrightarrow {u_{r}}+(r{\ddot \theta }+2{\dot r}{\dot \theta })\overrightarrow {u_{\theta }}+{\ddot z}\overrightarrow {u_{z}}=({\ddot r}-r{\dot \theta }^{2})\overrightarrow {u_{r}}+{\frac {1}{r}}{\frac {d(r^{2}{\dot \theta })}{dt}}\overrightarrow {u_{\theta }}+{\ddot z}\overrightarrow {u_{z}}\end{aligned}}

Il est à noter que l'on peut retrouver ces résultats de la manière suivante :

{\begin{aligned}{\dot {\overrightarrow {OM}}}&={\frac {d\overrightarrow {OM}}{dt}}={\frac {d(r\overrightarrow {u_{r}}+z\overrightarrow {u_{z}})}{dt}}={\frac {d(r\overrightarrow {u_{r}})}{dt}}+{\frac {d(z\overrightarrow {u_{z}})}{dt}}\\&={\frac {dr}{dt}}\overrightarrow {u_{r}}+r{\frac {d(\overrightarrow {u_{r}})}{dt}}+{\frac {dz}{dt}}\overrightarrow {u_{z}}+z{\frac {d(\overrightarrow {u_{z}})}{dt}}\\\\{\ddot {\overrightarrow {OM}}}&={\frac {d({\dot {\overrightarrow {OM}}})}{dt}}={\frac {d^{2}(\overrightarrow {OM})}{dt^{2}}}={\frac {d({\dot {r}}\overrightarrow {u_{r}}+r{\dot \theta }\overrightarrow {u_{\theta }}+{\dot z}\overrightarrow {u_{z}})}{dt}}={\frac {d({\dot r}\overrightarrow {u_{r}})}{dt}}+{\frac {d(r{\dot \theta }\overrightarrow {u_{\theta }})}{dt}}+{\frac {d({\dot z}\overrightarrow {u_{z}})}{dt}}\\&={\ddot r}\overrightarrow {u_{r}}+{\dot r}{\frac {d(\overrightarrow {u_{r}})}{dt}}+{\dot r}{\dot \theta }\overrightarrow {u_{\theta }}+r{\ddot \theta }\overrightarrow {u_{\theta }}+r{\dot \theta }{\frac {d(\overrightarrow {u_{\theta }})}{dt}}+{\ddot z}\overrightarrow {u_{z}}+{\dot z}{\frac {d(\overrightarrow {u_{z}})}{dt}}\\\\\end{aligned}}

etc. avec :

{\begin{aligned}{\frac {dr}{dt}}&={\dot r}\quad ;\quad {\frac {dz}{dt}}={\dot z}\quad ;\quad {\frac {d(\overrightarrow {u_{r}})}{dt}}={\frac {d(\overrightarrow {u_{r}})}{d\theta }}{\frac {d\theta }{dt}}={\dot \theta }\overrightarrow {u_{\theta }}\quad ;\quad {\frac {d(\overrightarrow {u_{\theta }})}{dt}}={\frac {d(\overrightarrow {u_{\theta }})}{d\theta }}{\frac {d\theta }{dt}}=-{\dot \theta }\overrightarrow {u_{r}}\quad ;\quad {\frac {d(\overrightarrow {u_{z}})}{dt}}=\overrightarrow {0}.\\\end{aligned}}

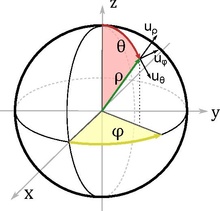
On se place dans le repère $(\overrightarrow {u_{\rho }},\overrightarrow {u_{\theta }},\overrightarrow {u_{\varphi }})$ .

Repère pour le calcul différentiel

Le volume infinitésimal s'écrit ${\text{d}}^{3}V=\rho ^{2}\sin \theta \,{\text{d}}\rho {\text{d}}\theta {\text{d}}\varphi$

Les surfaces infinitésimales :

L'élément de surface pour ρ constant s'écrit ${\text{d}}^{2}S_{\rho }=\rho ^{2}\sin \theta \,{\text{d}}\varphi \,{\text{d}}\theta$
L'élément de surface pour φ constant s'écrit ${\text{d}}^{2}S_{\varphi }=\rho \sin \theta \,{\text{d}}\theta \,{\text{d}}\rho$
L'élément de surface pour θ constant s'écrit ${\text{d}}^{2}S_{\theta }=\rho \,{\text{d}}\varphi \,{\text{d}}\rho$

Les vecteurs de la base comobile^[Quoi ?] $(\overrightarrow {u_{\rho }},\overrightarrow {u_{\theta }},\overrightarrow {u_{\varphi }})$ ont pour différentielles :

{\begin{aligned}{\text{d}}\overrightarrow {u_{\rho }}&={\text{d}}\theta \,{\vec {u}}_{\theta }+\sin \theta \,{\text{d}}\varphi \,{\vec {u}}_{\varphi }\\{\text{d}}\overrightarrow {u_{\theta }}&=-{\text{d}}\theta \,{\vec {u}}_{\rho }+\cos \theta \,{\text{d}}\varphi \,{\vec {u}}_{\varphi }\\{\text{d}}\overrightarrow {u_{\varphi }}&=-\sin \theta \,{\text{d}}\varphi \,{\vec {u}}_{\rho }-\cos \theta \,{\text{d}}\varphi \,{\vec {u}}_{\theta }\end{aligned}}

On en déduit les dérivées par rapport au temps :

{\begin{aligned}{\dot {\overrightarrow {u_{\rho }}}}&={\dot \theta }\,{\vec {u}}_{\theta }+{\dot \varphi }\,\sin \theta \,{\vec {u}}_{\varphi }\\{\dot {\overrightarrow {u_{\theta }}}}&={\dot \varphi }\,\cos \theta \,{\vec {u}}_{\varphi }-{\dot \theta }\,{\vec {u}}_{\rho }\\{\dot {\overrightarrow {u_{\varphi }}}}&=-{\dot \varphi }\,\sin \theta \,{\vec {u}}_{\rho }-{\dot \varphi }\,\cos \theta \,{\vec {u}}_{\theta }\end{aligned}}

L'opérateur nabla, servant au calcul du gradient, de la divergence et du rotationnel s'écrit

\overrightarrow {u_{\nabla }}=\left({\frac \partial {\partial \rho }},{\frac 1\rho }{\frac \partial {\partial \theta }},{\frac 1{\rho \sin \theta }}{\frac \partial {\partial \varphi }}\right)

Le laplacien s'en déduit :

\Delta ={\frac 1{\rho ^{2}}}{\frac \partial {\partial \rho }}\left(\rho ^{2}{\frac \partial {\partial \rho }}\right)+{\frac 1{\rho ^{2}\sin \theta }}{\frac \partial {\partial \theta }}\left(\sin \theta {\frac \partial {\partial \theta }}\right)+{\frac 1{\rho ^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}

${\begin{aligned}\overrightarrow {OM}&=\rho \,\overrightarrow {u_{\rho }}\\{\dot {\overrightarrow {OM}}}&={\dot \rho }\,\overrightarrow {u_{\rho }}+\rho {\dot \theta }\,\overrightarrow {u_{\theta }}+\rho \sin \theta \,{\dot \varphi }\,\overrightarrow {u_{\varphi }}\\{\ddot {\overrightarrow {OM}}}&=({\ddot \rho }-\rho {\dot \theta }^{2}-\rho {\dot \varphi }^{2}\sin ^{2}\theta )\,\overrightarrow {u_{\rho }}+(\rho {\ddot \theta }+2{\dot \rho }{\dot \theta }-\rho {\dot \varphi }^{2}\sin \theta \,\cos \theta )\,\overrightarrow {u_{\theta }}+(\rho {\ddot \varphi }\sin \theta +2{\dot \rho }{\dot \varphi }\sin \theta +2\rho {\dot \theta }{\dot \varphi }\cos \theta )\,\overrightarrow {u_{\varphi }}\end{aligned}}$

14/10/2016

0 J'aime 0 Poster un commentaire

rotationnel

rotationnel d'un vecteur

L'opérateur rotationnel est un opérateur différentiel aux dérivées partielles qui, à un champ vectoriel tridimensionnel, noté $\mathbf{A}$ ou $\vec{\mathrm{A}}$ , fait correspondre un autre champ noté au choix :

\overrightarrow{\operatorname{rot}}\ \vec{\mathrm{A}}

ou bien

\boldsymbol \nabla \wedge \mathbf{A}

ou bien

\boldsymbol \nabla \times \mathbf{A}

ou bien

\vec \nabla \wedge \vec{\mathrm{A}}

ou bien

\vec \nabla \times \vec{\mathrm{A}}

\boldsymbol \nabla \wedge \mathbf{F} = \begin{pmatrix} {\partial \mathrm{F}_z / \partial y} - {\partial \mathrm{F}_y / \partial z} \\ {\partial \mathrm{F}_x / \partial z} - {\partial \mathrm{F}_z / \partial x}\\ {\partial \mathrm{F}_y / \partial x} - {\partial \mathrm{F}_x / \partial y} \end{pmatrix}

\boldsymbol \nabla \wedge \mathbf{F} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \mathrm{F}_x & \mathrm{F}_y & \mathrm{F}_z \end{vmatrix}

14/10/2016

1 J'aime 0 Poster un commentaire

la divergence (div)

la divergence

En dimension 3 et en coordonnées cartésiennes, la divergence d'un champ de vecteurs ${\vec {A}}={\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}$ a pour expression1

\operatorname {div} {\vec {A}}={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\qquad (0)

Formellement, l'opérateur divergence appliqué à un champ vectoriel ${\vec {A}}$ peut s'interpréter comme produit scalaire du vecteur nabla ${\vec {A}}$ .

{\vec {\nabla }}\cdot {\vec {A}}=\operatorname {div} {\vec {A}}={\frac {\partial {A_{x}}}{\partial {x}}}+{\frac {\partial {A_{y}}}{\partial {y}}}+{\frac {\partial {A_{z}}}{\partial {z}}}

13/10/2016

0 J'aime 0 Poster un commentaire

le gradient d'une fonction scalaire

${\overrightarrow {\mathrm {grad} }}~f$ ou ${\overrightarrow {\nabla }}f$

${\overrightarrow {\operatorname {grad} }}\ {T}={\frac {\delta T}{\delta x}}\cdot {\vec {i}}.$

${\overrightarrow {\nabla }}T(x)=T'(x)\cdot {\vec {i}}={\frac {\mathrm {d} T}{\mathrm {d} x}}(x)\cdot {\vec {i}}.$

13/10/2016

1 J'aime 0 Poster un commentaire